随着现阶段越来越多的单元式幕墙的运用，薄壁开口式立柱成为单元式幕墙的主要受力构件，在建筑幕墙的结构计算中，大部分工程还是按照玻璃幕墙规范中的相关要求来计算结构的强度及刚度，而整体稳定这部分并未提及，铝合金受弯构件的整体稳定计算在《铝合金结构设计规范》GB 50429-2007（以下简称铝结构规范）中有单独的章节予以详细的规定，鉴于单元式幕墙中的立柱多采用开口式薄壁铝合金构件，这种构件的截面参数按照铝结构规范计算还是比较复杂的，其计算可以采用有限元软件屈曲分析求得屈曲因子，进而求其整体稳定系数[1]来计算构件的整体稳定性。具体步骤如下：
1. 首先利用已知条件，简化计算模型。
2. 建立有限元模型，添加屈曲分析（Buckling）工况，求得简支梁的屈曲因子。
3. 求得简支梁弯扭屈曲临界弯矩 [1]。
4. 基于铝结构规范附录C[2]，求得简支梁弯扭稳定相对长细比 ，最终求得简支梁受弯整体稳定系数 。
5. 利用铝结构规范相第6.2.2条[2]，来判断简支梁的整体稳定是否满足规范要求。
以下内容是我对单元式幕墙的主要受力构件的强度、刚度的计算过程及整体稳定计算的一点摸索和探讨。我们以一个实际工程中的案例来做一下分析，探讨一下开口式构件的整体稳定计算的重要性。

　　工程概况：
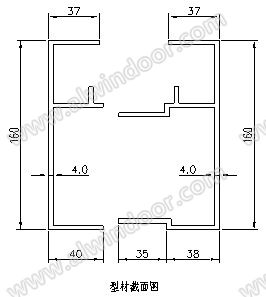
　　该项目位于南京市建邺区，主楼建筑幕墙最高高度为150.0米，裙楼建筑幕墙最高高度为25.05米，建筑幕墙面积为50,000平方米，主楼建筑幕墙采用单元式幕墙，立柱采用开口对插式铝合金公母料，该截面见右图：型材截面图（左边为母料，右边为公料），下面以母料来做一个计算演示；

通过计算单元式幕墙母料在考虑三道横梁的侧向支撑作用下才能满足的整体稳定的要求，当侧向支撑间距较大时，该母料的整体稳定将不能满足铝结构规范的要求，从而可以考虑采用其它方法来提高母料的整体稳定性能，加大壁厚就是其中的一种方法，但较经济性来讲，该方法又不是一个好的方法，所以如何考虑立柱的整体稳定性，需要综合考虑，下面我将就影响立柱整体稳定的因数做一组数值分析。
　　2.5.7 影响立柱整体稳定不足的因数有很多，平面外支撑只是其中的一种，构件的壁厚、翼缘的宽度、荷载、截面中的闭腔部分都能起到提高构件的整体稳定的目的，如何选择合理经济的方案需要结合建筑、幕墙形式等诸多因数，综合考虑；下面，我们建立几种不同壁厚、不同平面外支撑的几何模型，分别求其整体稳定系数，形成对比表格，以作数据分析；表中数据共计18组，分别采用三种不同壁厚、三种不同平面外支撑情况、两种截面形式（公料和母料），考虑到单元幕墙立柱的计算简化，荷载形式均为均布线荷载，指定的线荷载为1kN/m。分析程序采用SAP2000，利用其屈曲分析功能，得到每种模型的屈曲因子，按照铝结构规范的附录C计算、分析、列表，详细数据见表：《受弯构件整体稳定系数对比表》。

受弯构件整体稳定系数对比表

注：截面A为：母料；截面B为：公料； 为：无支撑最大间距；表中单位未注明者为：kN,m

　　通过表：《受弯构件整体稳定系数对比表》的数值分析，受弯构件的整体稳定与构件的诸多因数有关，在具体工程中要具体问题具体分析，总结一下：
1.构件的平面外支撑数量的增加（即无支撑间距的减小）对构件的整体稳定是有利的。
2.构件截面壁厚的增加对整体稳定是有利的。
3.构件翼缘的宽度的增加对整体稳定是有利的，但当翼缘宽度与厚度的比值达到一定数值后，构件的局部失稳将较构件的整体失稳先发生，也就意味着如果一味地增加翼缘的宽度对构件的整体稳定是没有太大意义的，在考虑成本的情况下，这一点是需要注意的。
4.工程中经常遇到构件承载力不足时，往往设计人员仅通过增加构件主轴方向的高度来满足规范的设计要求，对开口式构件，此方法在使用时尤其要慎重，一定要注意构件的整体稳定验算。
3 结 语
本文是单元式幕墙开口截面立柱的整体稳定计算方法的一个初探，其方法仅供大家在以后对单元式幕墙结构计算分析中做一点参考，同时鉴于构件式幕墙的受力构件通常采用闭腔结构，故其整体稳定性较好，所以幕墙规范中并未规定对其整体稳定计算的要求，只通过规定其最小壁厚来满足构件的局部要求。而开口式构件的整体稳定较差，尤其对利用率较高的构件应当验算其整体稳定能否满足要求。
本文模拟平面外支撑采用的方法是约束构件在横梁位置构件的平面外位移，这与实际的结构受力形式存在一定的误差，对构件的整体稳定有一定的影响，该部分的研究也应当做更深入的研究，本文不再深入。
参考文献
[1] 王治明，赵华.一种基于有限元软件屈曲分析求解铝合金受弯构件整体稳定系数的方法[J] .2011年全国铝门窗幕墙行业年会论文集，2011
[2] GB 50429-2007 铝合金结构设计规范[S] .